publications

2025

1. arxiv

   

   From Data to Rewards: a Bilevel Optimization Perspective on Maximum Likelihood Estimation

   Abdelhakim Benechehab, Gabriel Singer, Corentin Léger, and 5 more authors

   Preprint, Oct 2025

   Abs Bib Code

   Generative models form the backbone of modern machine learning, underpinning state-of-the-art systems in text, vision, and multimodal applications. While Maximum Likelihood Estimation has traditionally served as the dominant training paradigm, recent work have highlighted its limitations, particularly in generalization and susceptibility to catastrophic forgetting compared to Reinforcement Learning techniques, such as Policy Gradient methods. However, these approaches depend on explicit reward signals, which are often unavailable in practice, leaving open the fundamental problem of how to align generative models when only high-quality datasets are accessible. In this work, we address this challenge via a Bilevel Optimization framework, where the reward function is treated as the optimization variable of an outer-level problem, while a policy gradient objective defines the inner-level. We then conduct a theoretical analysis of this optimization problem in a tractable setting and extract insights that, as we demonstrate, generalize to applications such as tabular classification and model-based reinforcement learning.

   @article{benechehab2025nllpo,
     title = {From Data to Rewards: a Bilevel Optimization Perspective on Maximum Likelihood Estimation},
     author = {Benechehab, Abdelhakim and Singer, Gabriel and Léger, Corentin and Attia El Hili, Youssef and Paolo, Giuseppe and Thomas, Albert and Filippone, Maurizio and Kégl, Balàzs},
     journal = {Preprint},
     year = {2025},
     month = oct,
     day = {10},
     selected = true,
   }

2. workshop @ NeurIPS

   

   In-Context Meta-Learning with Large Language Models for Automated Model and Hyperparameter Selection

   Youssef Attia El Hili, Albert Thomas, Abdelhakim Benechehab, and 3 more authors

   NeurIPS Workshop LLM-eval, Sep 2025

   Abs Bib PDF

   Model and hyperparameter selection is a critical yet costly step in machine learning, often requiring expert intuition or extensive search. We investigate whether large language models (LLMs) can reduce this cost by acting as in-context meta-learners that generalize across tasks to propose effective model-hyperparameter choices without iterative optimization. Each task is represented as structured metadata, and we prompt an LLM under two strategies: Zero-Shot, using only the target task metadata, and Meta-Informed, which augments the prompt with metadata–recommendation pairs from prior tasks. Evaluated on 22 tabular Kaggle challenges, Meta-Informed prompting outperforms Zero-Shot and hyperparameter optimization baselines, approaching expert AutoML blends while yielding interpretable reasoning traces and efficiency gains under tight training budgets. These results suggest that LLMs can transfer knowledge across tasks to guide automated model selection, establishing model and hyperparameter selection as a concrete testbed for studying emergent adaptation beyond language domains.

   @article{hili2025incontext,
     title = {In-Context Meta-Learning with Large Language Models for Automated Model and Hyperparameter Selection},
     author = {Attia El Hili, Youssef and Thomas, Albert and Benechehab, Abdelhakim and Léger, Corentin and Ancourt, Corinne and Kégl, Balàzs},
     journal = {NeurIPS Workshop LLM-eval},
     year = {2025},
     month = sep,
     day = {22},
     selected = true,
   }

3. ICML

   

   AdaPTS: Adapting Univariate Foundation Models to Probabilistic Multivariate Time Series Forecasting

   Abdelhakim Benechehab, Vasilii Feofanov, Giuseppe Paolo, and 3 more authors

   ICML, May 2025

   Abs arXiv Bib PDF Code Poster

   Pre-trained foundation models (FMs) have shown exceptional performance in univariate time series forecasting tasks. However, several practical challenges persist, including managing intricate dependencies among features and quantifying uncertainty in predictions. This study aims to tackle these critical limitations by introducing adapters; feature-space transformations that facilitate the effective use of pre-trained univariate time series FMs for multivariate tasks. Adapters operate by projecting multivariate inputs into a suitable latent space and applying the FM independently to each dimension. Inspired by the literature on representation learning and partially stochastic Bayesian neural networks, we present a range of adapters and optimization/inference strategies. Experiments conducted on both synthetic and real-world datasets confirm the efficacy of adapters, demonstrating substantial enhancements in forecasting accuracy and uncertainty quantification compared to baseline methods. Our framework, AdaPTS, positions adapters as a modular, scalable, and effective solution for leveraging time series FMs in multivariate contexts, thereby promoting their wider adoption in real-world applications.

   @article{benechehab2025adapts,
     title = {AdaPTS: Adapting Univariate Foundation Models to Probabilistic Multivariate Time Series Forecasting},
     author = {Benechehab, Abdelhakim and Feofanov, Vasilii and Paolo, Giuseppe and Thomas, Albert and Filippone, Maurizio and Kégl, Balázs},
     journal = {ICML},
     year = {2025},
     month = may,
     day = {1},
     selected = true,
   }

4. ICLR

   

   Zero-shot Model-based Reinforcement Learning using Large Language Models

   Abdelhakim Benechehab, Youssef Attia El Hili, Ambroise Odonnat, and 6 more authors

   ICLR, Jan 2025

   Abs arXiv Bib PDF Code Poster Slides Website

   The emerging zero-shot capabilities of Large Language Models (LLMs) have led to their applications in areas extending well beyond natural language processing tasks. In reinforcement learning, while LLMs have been extensively used in text-based environments, their integration with continuous state spaces remains understudied. In this paper, we investigate how pre-trained LLMs can be leveraged to predict in context the dynamics of continuous Markov decision processes. We identify handling multivariate data and incorporating the control signal as key challenges that limit the potential of LLMs’ deployment in this setup and propose Disentangled In-Context Learning (DICL) to address them. We present proof-of-concept applications in two reinforcement learning settings: model-based policy evaluation and data-augmented off-policy reinforcement learning, supported by theoretical analysis of the proposed methods. Our experiments further demonstrate that our approach produces well-calibrated uncertainty estimates.

   @article{benechehab2024zero,
     title = {Zero-shot Model-based Reinforcement Learning using Large Language Models},
     author = {Benechehab, Abdelhakim and Hili, Youssef Attia El and Odonnat, Ambroise and Zekri, Oussama and Thomas, Albert and Paolo, Giuseppe and Filippone, Maurizio and Redko, Ievgen and K{\'e}gl, Bal{\'a}zs},
     journal = {ICLR},
     year = {2025},
     month = jan,
     day = {15},
     selected = true,
   }

2024

1. arxiv

   

   Large Language Models as Markov Chains

   Oussama Zekri, Ambroise Odonnat, Abdelhakim Benechehab, and 3 more authors

   Preprint, Oct 2024

   Abs arXiv Bib PDF

   Large language models (LLMs) have proven to be remarkably efficient, both across a wide range of natural language processing tasks and well beyond them. However, a comprehensive theoretical analysis of the origins of their impressive performance remains elusive. In this paper, we approach this challenging task by drawing an equivalence between generic autoregressive language models with vocabulary of size T and context window of size K and Markov chains defined on a finite state space of size O(T^K). We derive several surprising findings related to the existence of a stationary distribution of Markov chains that capture the inference power of LLMs, their speed of convergence to it, and the influence of the temperature on the latter. We then prove pre-training and in-context generalization bounds and show how the drawn equivalence allows us to enrich their interpretation. Finally, we illustrate our theoretical guarantees with experiments on several recent LLMs to highlight how they capture the behavior observed in practice.

   @article{zekri2024large,
     title = {Large Language Models as Markov Chains},
     author = {Zekri, Oussama and Odonnat, Ambroise and Benechehab, Abdelhakim and Bleistein, Linus and Boull{\'e}, Nicolas and Redko, Ievgen},
     journal = {Preprint},
     year = {2024},
     month = oct,
     day = {3},
     selected = true,
   }

2. workshop @ ICML

   

   Can LLMs predict the convergence of Stochastic Gradient Descent?

   Oussama Zekri, Abdelhakim Benechehab, and Ievgen Redko

   ICML Workshop ICL, Jun 2024

   Abs Bib PDF Poster

   Large-language models are notoriously famous for their impressive performance across a wide range of tasks. One surprising example of such impressive performance is a recently identified capacity of LLMs to understand the governing principles of dynamical systems satisfying the Markovian property. In this paper, we seek to explore this direction further by studying the dynamics of stochastic gradient descent in convex and non-convex optimization. By leveraging the theoretical link between the SGD and Markov chains, we show a remarkable zero-shot performance of LLMs in predicting the local minima to which SGD converges for previously unseen starting points. On a more general level, we inquire about the possibility of using LLMs to perform zero-shot randomized trials for larger deep learning models used in practice.

   @article{zekri2024can,
     title = {Can LLMs predict the convergence of Stochastic Gradient Descent?},
     author = {Zekri, Oussama and Benechehab, Abdelhakim and Redko, Ievgen},
     journal = {ICML Workshop ICL},
     year = {2024},
     month = jun,
     day = {18},
     selected = true,
   }

3. workshop @ RLC

   

   A Study of the Weighted Multi-step Loss Impact on the Predictive Error and the Return in MBRL

   Abdelhakim Benechehab, Albert Thomas, Giuseppe Paolo, and 2 more authors

   RLC Workshop ICBINB, Jun 2024

   Abs Bib PDF Video Poster Slides

   In model-based reinforcement learning, most algorithms rely on simulating trajectories from one-step models of the dynamics learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as the length of the trajectory grows. In this paper we tackle this issue by using a multi-step objective to train one-step models. Our objective is a weighted sum of the mean squared error (MSE) loss at various future horizons. We find that this new loss is particularly useful when the data is noisy (additive Gaussian noise in the observations), which is often the case in real-life environments. We show in a variety of tasks (environments or datasets) that the models learned with this loss achieve a significant improvement in terms of the averaged R2-score on future prediction horizons. To our surprise, in the pure batch reinforcement learning setting, we find that the multi-step loss-based models perform only marginally better than the baseline. Furthermore, this improvement is only observed for small loss horizons, unlike the trend present with the R2-score on the respective datasets.

   @article{benechehab2024study,
     title = {A Study of the Weighted Multi-step Loss Impact on the Predictive Error and the Return in MBRL},
     author = {Benechehab, Abdelhakim and Thomas, Albert and Paolo, Giuseppe and Filippone, Maurizio and K{\'e}gl, Bal{\'a}zs},
     journal = {RLC Workshop ICBINB},
     year = {2024},
     month = jun,
     day = {7},
     selected = true,
   }

4. blogpost @ ICLR

   

   Fair Model-Based Reinforcement Learning Comparisons with Explicit and Consistent Update Frequency

   Albert Thomas, Abdelhakim Benechehab, Giuseppe Paolo, and 1 more author

   ICLR Blogpost, Feb 2024

   Abs Bib Blog Poster

   Implicit update frequencies can introduce ambiguity in the interpretation of model-based reinforcement learning benchmarks, obscuring the real objective of the evaluation. While the update frequency can sometimes be optimized to improve performance, real-world applications often impose constraints, allowing updates only between deployments on the actual system. This blog post emphasizes the need for evaluations using consistent update frequencies across different algorithms to provide researchers and practitioners with clearer comparisons under realistic constraints.

   @article{thomas2024fair,
     title = {Fair Model-Based Reinforcement Learning Comparisons with Explicit and Consistent Update Frequency},
     author = {Thomas, Albert and Benechehab, Abdelhakim and Paolo, Giuseppe and K{\'e}gl, Bal{\'a}zs},
     journal = {ICLR Blogpost},
     year = {2024},
     month = feb,
     day = {16},
   }

2023

1. arXiv

   

   Multi-timestep models for Model-based Reinforcement Learning

   Abdelhakim Benechehab, Giuseppe Paolo, Albert Thomas, and 2 more authors

   Preprint, Feb 2023

   Abs arXiv Bib PDF

   In model-based reinforcement learning (MBRL), most algorithms rely on simulating trajectories from one-step dynamics models learned on data. A critical challenge of this approach is the compounding of one-step prediction errors as length of the trajectory grows. In this paper we tackle this issue by using a multi-timestep objective to train one-step models. Our objective is a weighted sum of a loss function (e.g., negative log-likelihood) at various future horizons. We explore and test a range of weights profiles. We find that exponentially decaying weights lead to models that significantly improve the long-horizon R2 score. This improvement is particularly noticeable when the models were evaluated on noisy data. Finally, using a soft actor-critic (SAC) agent in pure batch reinforcement learning (RL) and iterated batch RL scenarios, we found that our multi-timestep models outperform or match standard one-step models. This was especially evident in a noisy variant of the considered environment, highlighting the potential of our approach in real-world applications.

   @article{benechehab2023multi,
     title = {Multi-timestep models for Model-based Reinforcement Learning},
     author = {Benechehab, Abdelhakim and Paolo, Giuseppe and Thomas, Albert and Filippone, Maurizio and K{\'e}gl, Bal{\'a}zs},
     journal = {Preprint},
     year = {2023},
   }

2022

1. arXiv

   

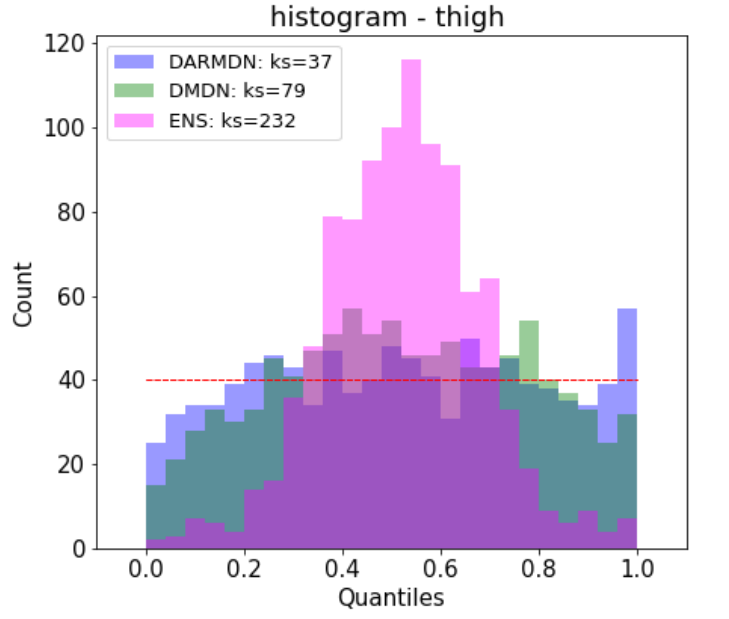
   Deep autoregressive density nets vs neural ensembles for model-based offline reinforcement learning

   Abdelhakim Benechehab, Albert Thomas, and Balázs Kégl

   Preprint, Feb 2022

   Abs arXiv Bib PDF

   We consider the problem of offline reinforcement learning where only a set of system transitions is made available for policy optimization. Following recent advances in the field, we consider a model-based reinforcement learning algorithm that infers the system dynamics from the available data and performs policy optimization on imaginary model rollouts. This approach is vulnerable to exploiting model errors which can lead to catastrophic failures on the real system. The standard solution is to rely on ensembles for uncertainty heuristics and to avoid exploiting the model where it is too uncertain. We challenge the popular belief that we must resort to ensembles by showing that better performance can be obtained with a single well-calibrated autoregressive model on the D4RL benchmark. We also analyze static metrics of model-learning and conclude on the important model properties for the final performance of the agent.

   @article{benechehab2022deep,
     title = {Deep autoregressive density nets vs neural ensembles for model-based offline reinforcement learning},
     author = {Benechehab, Abdelhakim and Thomas, Albert and K{\'e}gl, Bal{\'a}zs},
     journal = {Preprint},
     year = {2022},
   }